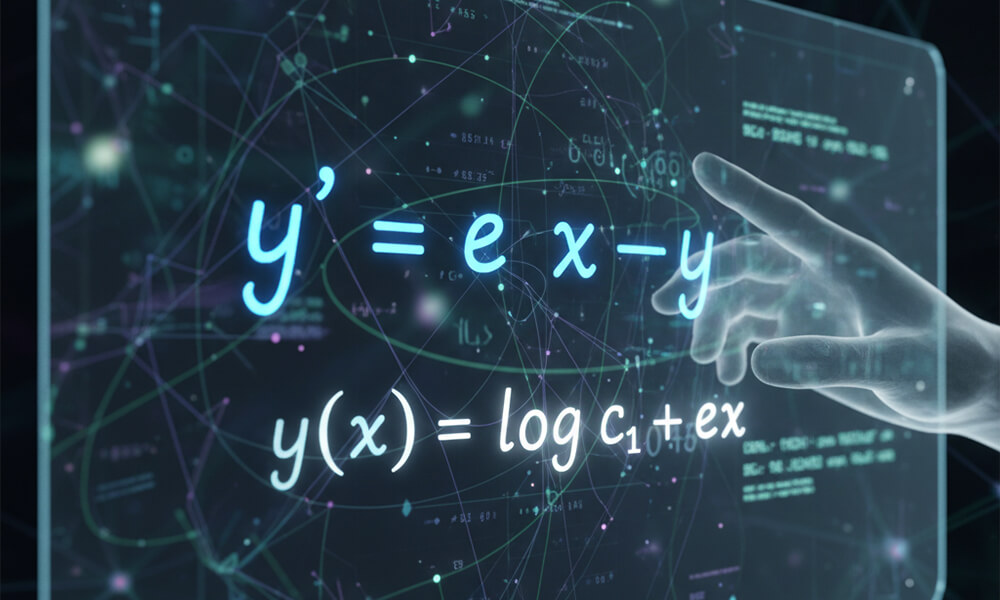Wolfram Alpha Plugin for ChatGPT: Solving Differential Equations

In the previous post it was seen that ChatGPT 4 had struggled to find the general solution of a differential equation, giving twice wrong solutions and only the third attempt ChatGPT 4 had managed to give the correct solution. The reason is that ChatGPT 4 is not designed to solve mathematical problems, however it tries and often, but not always, succeeds. For this reason you should never trust yourself blindly but ask ChatGPT for all the intermediate steps and check them very carefully.
In this post I tried to submit the same ordinary differential equation always to ChatGPT 4 but assisted by the plugin Wolfram Alpha (which is designed to solve mathematical problems) and the right solution arrived, as I expected, at the first attempt.

The equation is the same as in the previous post:

\(y’ = e^{x – y} \)

and the right solution is:

\(y(x) = log(c_1 + e^x) \)

Wolfram Alpha plugin

I installed the Wolfram Alpha plugin following the instruction at this link: https://www.wolfram.com/wolfram-plugin-chatgpt/
Then, on ChatGPT 4, with Wolfram Alpha plugin enabled, my prompt was:

Solve this following ordinary differential equation: y’ = e^(x-y)

and the ChatGPT answer was:

The solution to the ordinary differential equation \(y’ = e^{x – y} \) is given by \(y(x) = \log(c_1 + e^x) \), where \(c_1 \) is an arbitrary constant. This is a first-order nonlinear ordinary differential equation.

And this time ChatGPT 4 assisted by Wolfram Alpha found right solution immediately.
Then I prompted:

Show me the steps

and ChatGPT 4 (with Wolfram Alpha plugin) was:

To solve the differential equation \(y’ = e^{x – y} \), we can use the method of separation of variables. Here are the steps:

1. Rewrite the Equation: Start by expressing the differential equation in a form that allows separation of variables. The given equation is \(y’ = e^{x – y} \).

2. Separate Variables: We want to get all the \(y \) terms on one side and all the \(x \) terms on the other side. To do this, we can write \(y’ \) as \(\frac{dy}{dx} \) and rearrange the equation:
\(\frac{dy}{dx} = e^{x – y} \)
Now, multiply both sides by \(e^y \) to get:
\(e^y \frac{dy}{dx} = e^x \)
3. Integrate Both Sides: Next, integrate both sides of the equation. On the left side, integrate with respect to \(y \), and on the right side, integrate with respect to \(x \):
\(\int e^y \, dy = \int e^x \, dx \)
This gives:
\(e^y = e^x + C \) where \(C \) is the constant of integration.
4. Solve for \(y \): Finally, solve for \(y \) by taking the natural logarithm of both sides:
\(y = \ln(e^x + C) \)

So, the general solution to the differential equation \(y’ = e^{x – y} \) is \(y(x) = \ln(e^x + C) \), where \(C \) is an arbitrary constant.

The Cauchy problem

Having found the right solution, I wanted to solve a Cauchy problem, so I prompted:

What is the specific solution having the condition y(0)=1 ?

and ChatGPT 4 & Wolfram Alpha plugin answered:

The specific solution to the differential equation \(y’ = e^{x – y} \) with the initial condition \(y(0) = 1 \) is given by: \(y(x) = \log(e^x -1 + e) \)

that is right; finally I asked for a graph of this solution with the prompt:

Plot this solution

and this is what I got:

Here is the plot of the solution \(y(x) = \log(e^x -1 + e) \) for the range \(x \) from \(-2 \) to \(2 \):

CONCLUSION

The combination of ChatGPT 4 and the Wolfram Alpha plugin allows to obtain solutions to mathematical problems much more reliable than those that ChatGPT 4 can solve alone, and that’s because Wolfram Alpha is a tool designed to solve mathematical problems while ChatGPT 4 is a chatbot.

Wolfram Alpha Plugin for ChatGPT: Solving Differential Equations

Wolfram Alpha plugin

The Cauchy problem

CONCLUSION

NablaVis: an interactive educational tool to visualize three applications of Stokes’ Theorem

ChatGPT 4 Solving Ordinary Differential Equations